I Parcial
Introducción a los cálculos de ingeniería química
Objetivos: sumar, restar, multiplicar y dividir unidades asociadas a cifras. especificar unidades básicas y derivadas del SI y sistemas americanos de medidas. Convertir un conjunto de unidades de una ecuación en otro conjunto equivalente.
1.1 Dimensiones Fundamentales
¿Qué son las unidades y las dimensiones, y en qué se distinguen?
Las dimensiones son nuestros conceptos básicos de medición, como longitud, tiempo, masa, temperatura, etc.; las unidades son la forma de expresar las dimensiones, como pies o centímetros para la longitud, u horas o segundos para el tiempo. Al anexar unidades a todos los números que no son fundamentalmente dimensionales, se obtienen los siguientes beneficios prácticos:
1 ) Menor probabilidad de invertir, sin darse cuenta, una parte del cálculo.
2 ) Reducción en el número de cálculos intermedios y en el tiempo durante la resolución de problemas.
3) Un enfoque lógico del problema, en lugar de limitarse a recordar una fórmula e insertarle números.
4) Fácil interpretación del significado físico de los números empleados.
Unidades Del SI
Unidades Derivadas
Unidades sistema ingles
Conversión de unidades:
Ejemplo 1:
Si un avión viaja al doble de la velocidad del sonido ¿cual es su velocidad en millas por hora?
*Velocidad del sonido: 1100 ft/s
* 1 Milla: 5280 ft/s
* 1 hora: 3600 seg 2|1100ft/s|*|1mi/5280ft|*|3600s/1h| = 1500mi/h
Ejemplo 2:
¿ Cuanta energía potencial en lbf.ft tiene un tambor de 100 lb suspendido 10ft sobre la superficie de la tierra con frecuencia a dicha superficie?
Epotencial: m*g*h
Epot = (100lb)*(32.2ft/s^2)*(10ft) = 1000 lbf.ft
El uso correcto de las dimensiones al resolver los problemas no solo es justificable desde el punto de vista lógico también ayuda a encontrar el camino de análisis apropiado que nos lleva a los estudiantes desde la información que disponemos hasta la que debemos obtener en la solución final.
Por lo tanto este tema es de mucha ayuda para cualquier estudiante ya que siempre se tiene dificultades y deficiencias con las unidades en las que debemos trabajar en los problemas a resolver. el conocimiento adquirido sobre las unidades y dimensiones siempre será de gran utilidad.
1.2 Presión
La presión se define como fuerza normal por unidad de área. P= F/A
Terminos:
*Presión Atmosférica: Presion del aire y medio atmosférico que nos rodea el cual varia dia a dia.
*Presion Barometrica: Es la misma que esta presente en la atmosfera y para medirla se utiliza un barómetro.
*Presion Absoluta: Medida de la presión con respecto al vacio total.
*Presion Manometrica: Presion expresada como cantidad medida con respecto a la presión atmosférica.
*Vacio: Presion menor a la atmosfera.
La presión depende de dos factores:
-Altura
-Temperatura
Ejemplo:
Un manometro de Hg se encuentra adaptado a un tanque se sabe que el tanque se encuentra a una presión menor que la atmosferica. Si el manometro registra una lectura de 25.4 pulgadas de Hg vacio y el baromtreo indica 14.79 psia ¿ Cual será la presión absoluta en el tanque?
Reflexión:
El estudio de la presión es un tema muy importante ya que es un factor influyente en muchos procesos, es decir, que puede modificar las circunstancias en que están sucediendo un tratamiento o procedimiento por eso en la industria es de utilidad saberlo por que podemos enfrentarnos a diferentes tipos de bombas sometidas a determinadas presiones y por ende se puede enfrentar a cambios de presión que necesitaran la realización de cálculos.
1.3 Propiedades De Las Sustancias
Densidad: es la razón de la masa por unidad de volumen, se expresa como kg/m3 o lb/ft3.
Se expresa tanto para un valor numérico como por unidades adecuadas. para determinar la densidad de una sustancia, es preciso conocer tanto su volumen como su masa. Las densidades de los liquidos y los solidos no cambian significativamente con la presión en condiciones ordinarias pero si cambian con la temperatura.
Por lo tanto la masa y el volumen de una sustancia la podemos evaluar así:
> masa: m = ρ . V
> Volumen: V = m / ρ
*Densidad Relativa: es una comparación de la densidad de una sustancia con la densidad de otra que se toma como referencia. Ambas densidades se expresan en las mismas unidades y en iguales condiciones de temperatura y presión.
*Peso Especifico: Se llama peso específico al peso que posee una sustancia en un determinado volumen.
siendo,
, el peso específico;
, el peso de la sustancia;
, el volumen de la sustancia;
, la densidad de la sustancia;
, la masa de la sustancia;
, la aceleración de la gravedad
*Volumen Específico (
) es el volumen ocupado por unidad de masa de un material. Es el inverso de la densidad, por lo cual no dependen de la cantidad de materia. Ejemplos: dos pedazos de hierro de distinto tamaño tienen diferente peso y volumen pero el peso específico de ambos será igual. Este es independiente de la cantidad de materia que es considerada para calcularlo
) es el volumen ocupado por unidad de masa de un material. Es el inverso de la densidad, por lo cual no dependen de la cantidad de materia. Ejemplos: dos pedazos de hierro de distinto tamaño tienen diferente peso y volumen pero el peso específico de ambos será igual. Este es independiente de la cantidad de materia que es considerada para calcularlo
Donde, 
es el volumen, 
es la masa y 
es la densidad del material.
es el volumen, es la masa y es la densidad del material.
Se expresa en unidades de volumen sobre unidades de masa.
- Ejemplo:
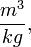
. - Densidades de alguno líquidos
¿Cuál es la densidad de un material si tiene una masa de 12 libras y un volumen de 6 m cúbicos?
Solución:
- Primero tenemos que pasar la masa de libras a kilogramos
Sabemos que: 1 libra = 0,45 Kilogramos
Entonces: 12 libra = 0,45 x 12 Kg = 5,4 Kg
masa (m) = 5,4 Kg
V = 6 m3
- Reemplazando en la formula de la densidad:
ρ = m / V
ρ = 5,4 Kg / 6 m3
ρ = 0,9 Kg / m3
*Viscosidad
Es la resistencia que presenta un fluido a fluir.
La viscosidad solo se manifiesta en líquidos en movimiento, se ha definido la viscosidad como la relación existente entre el esfuerzo cortante y el gradiente de velocidad.
La viscosidad se divide en dos:
* Viscosidad Cinemática
*Viscosidad Dinámica
Se miden en:
SI: N/m2
Para calcular la viscosidad cinemática basta con dividir la viscosidad dinámica por la densidad del fluido.
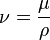
Ejemplo:
Dos superficies planas de grandes dimensiones están separadas 25mm y el espacio entre ellas esta lleno con un liquido cuya viscosidad absoluta es 0.98 N/m2 = 0.98 Pa.s. Suponiendo que el gradiente de velocidad es lineal ¿Que fuerza se requiere para arrastar una placa de muy poco espesor y 40dm2 de área a la velocidad constante de 32 cm/s. Si la placa dista 8 mm de una de las superficies?
Para producirse dos esfuerzos cortantes, se necesitan dos fuerzas para mover la placa
Ft=F1 + F2
F1= 0.98 N/m2 0.4m2*( 0.32 ms / 0.017 m) = 7.37 F2= 0.98 N/m2 0.4m2*( 32ms / 0.008m) = 15.68
FT= 15.68 N + 7.37 N = 23.05
Conocer la viscosidad de un fluido es importante, para el diseño de equipo de procesos, tambien es importante conocer sus unidades y poder manejarlas, las viscosidades son de gran importancia para establecer condiciones de transporte de fluidos, intercambio de calor o secado y como parametro de control de calidad, ya que la viscosidad es una propiedad fisicoquimica que influye en la textura y percepcion de un fluido.
Exposición #1
TemperaturaEs una magnitud escalar asociado con la cantidad de energía este es independiente de la cantidad de la muestra.
Tipos de Termómetro:
De dilatación
Resistencia
Termistor: Es un sensor de temperatura por resistencia
Termopar: Es utilizado para medir temperatura conectados a un controlador digital.
TemperaturaEs una magnitud escalar asociado con la cantidad de energía este es independiente de la cantidad de la muestra.
Tipos de Termómetro:
De dilatación
Resistencia
Termistor: Es un sensor de temperatura por resistencia
Termopar: Es utilizado para medir temperatura conectados a un controlador digital.
Escalas de temperatura mas utilizadas
Celsius
Farenheit
Kelvin
Rankine
1.4 Inflamabilidad, toxicidad y autoignicion
El punto de inflamacion de una sustancia, temperatura del aire a la que el vapor esta sobre una sustancia producira un destello o explotara en presencia de una flama.
Normas OSHA:
a) De acuerdo a su toxicidad
b) Inflamibilidad
c) Grado de reactividad
d) Pnto de inflamibilidad
Grado de toxicidad:
4 muerte
3 lesion mayor o temporal
2 lesion menor o temporal
1 lesion menor facil reversible
0 no hay efectos toxicos
Inflamabilidad:
4 forma de mezclas explosivas en el aire
3 se puede encender al ambiente
2 materiales a someter a temperaturas moderadas
1 materiales a someter a temperaturas elevadas
0 no arden
Reflexion:
Para un quimico industrial es de mucha importancia saber el manejo de muchas sustancias que pueden ser peligrosas por su grado de inflamabilidad que pueden presentar estas al estar en contactos algun tipo de ambiente, es por eso que se dispone de tablas, graficos que nos guian a conocer las caracteristicas de una sustancia y que resultados se pueden obtener y como se comportan.
1.5 Perdidas Primarias Y Secundarias
Perdidas primarias
Pérdidas primarias: Se producen cuando el fluido se pone en contacto con la superficie de la tubería. Esto provoca que se rocen unas capas con otras (flujo laminado) o de partículas de fluidos entre sí (flujo turbulento). Estas pérdidas se realizan solo en tramos de tuberías horizontal y de diámetro constante.
Perdidas secundarias
Se producen en transiciones de la tubería (estrechamiento o expansión) y en toda clase de accesorios (válvulas, codos). En el cálculo de las pérdidas de carga en tuberías son importantes dos factores:
*Que la tubería sea lisa o rugosa.
* Que el fluido sea laminar o turbulento
Ecuacion de perdidas primarias
La forma general de la ecuación de Darcy-Weisbach es:
siendo:
= pérdida de carga debida a la fricción. (m)
= factor de fricción de Darcy. (adimensional)
= longitud de la tubería. (m)
= diámetro de la tubería. (m) = velocidad media del fluido. (m/s)
= aceleración de la gravedad ≈ 9,80665 m/s².2
Aplicación de ecuación de Bernoulli:
La ecuación de Bernoulli es aplicable a fluidos no viscosos, incompresibles en los que no existe aportación de trabajo exterior, por ejemplo mediante una bomba, ni extracción de trabajo exterior, por ejemplo mediante una turbina. De todas formas, a partir de la conservación de la Cantidad de movimiento para fluidos incompresibles se puede escribir una forma más general que tiene en cuenta fricción y trabajo:
donde:
es el peso específico (
). Este valor se asume constante a través del recorrido al ser un fluido incompresible.
trabajo externo que se le suministra (+) o extrae al fluido (-) por unidad de caudal másico a través del recorrido del fluido.- disipación por fricción a través del recorrido del fluido.
- Los subíndices
y 
indican si los valores están dados para el comienzo o el final del volumen de control respectivamente. - g = 9,81 m/s2.
No de Reynolds
El número de Reynolds relaciona la densidad, viscosidad, velocidad y dimensión típica de un flujo en una expresión adimensional, que interviene en numerosos problemas de dinámica de fluidos. Dicho número o combinación adimensional aparece en muchos casos relacionado con el hecho de que el flujo pueda considerarse laminar (número de Reynolds pequeño) o turbulento (número de Reynolds grande).
Para un fluido que circula por el interior de una tubería circular recta, el número de Reynolds viene dado por:
o equivalentemente por:
donde:
: densidad del fluido
: velocidad característica del fluido: diámetro de la tubería a través de la cual circula el fluido o longitud característica del sistema
: viscosidad dinámica del fluido
: viscosidad cinemática del fluido (m²/s)
Además el número de Reynolds permite predecir el carácter turbulento o laminar en ciertos casos.
En conductos o tuberías (en otros sistemas, varía el Reynolds límite):
Si el número de Reynolds es menor de 2000 el flujo será laminar y si es mayor de 2000 el flujo será turbulento. El mecanismo y muchas de las razones por las cuales un flujo es laminar o turbulento es todavía hoy objeto de especulación.
*El factor de friccion para flujo laminar será: f = 64/ Re
*Para fujo turbulento se tiene 2 subdivisiones: según la rugosidad y N° de Reynolds
Diagrama De Moody
El diagrama de Moody es la representación gráfica en escala doblemente logarítmica del factor de fricción en función del número de Reynolds y la rugosidad relativa de una tubería, diagrama hecho por Lewis Ferry Moody.
1.6 Medidas De Caudales
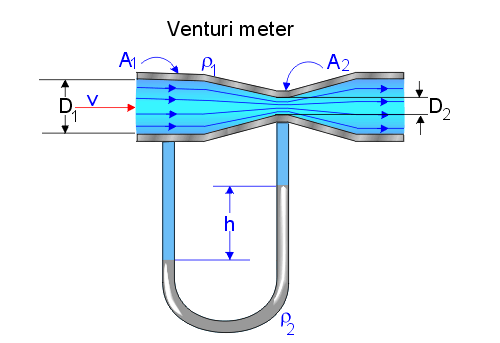
El efecto Venturi se explica por el Principio de Bernoulli y el principio de continuidad de masa. Si el caudal de un fluido es constante pero la sección disminuye, necesariamente la velocidad aumenta tras atravesar esta sección. Por el teorema de la conservación de la energía mecánica, si la energía cinética aumenta, la energía determinada por el valor de la presión disminuye forzosamente.
Efectivamente, según el principio de Bernoulli:
donde:
= velocidad del fluido en la sección considerada.
= aceleración gravitatoria, g ≈ 9,81 m/s2.
= presión en cada punto de la línea de corriente.
es el peso específico (). Este valor se asume constante a lo largo del recorrido cuando se trata de un fluido incompresible.
= altura, en vertical, sobre una cota de referencia.
Los subíndices y indican que los valores se toman en un punto 1 y en otro punto 2, a lo largo de la conducción
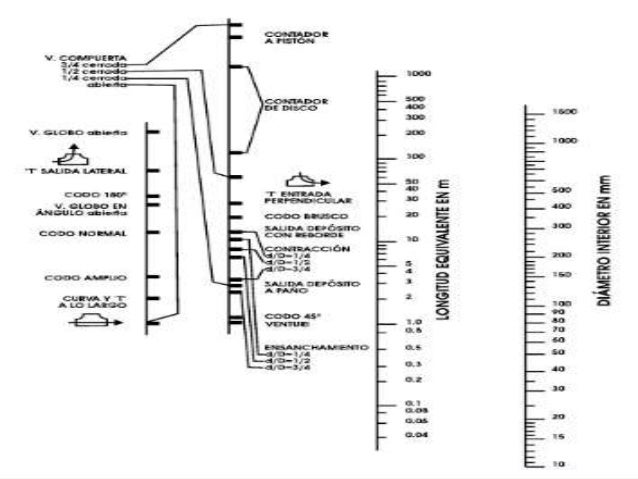
Nomograma de longitud equivalente
= velocidad del fluido en la sección considerada.
= aceleración gravitatoria, g ≈ 9,81 m/s2.
= presión en cada punto de la línea de corriente.
es el peso específico (). Este valor se asume constante a lo largo del recorrido cuando se trata de un fluido incompresible.
= altura, en vertical, sobre una cota de referencia.
Los subíndices y indican que los valores se toman en un punto 1 y en otro punto 2, a lo largo de la conducción
Nomograma de longitud equivalente
Ejemplo:
Para transportar un aceite de un deposito A a otro B con un Q= 200L/min es necesario instalar una bomba cuya potencia se desea determinar, sabiendo que el rendimiento es del 60%. La tubería de conducción es de hierro de 3 pulgadas y longitud 300 metros los accesorios de la instalación son:
2 válvulas de asiento, 1 empalme de 180°, 8 codos angulares, el nivel de aceite en B se mantiene 12 metros por encima de A. La densidad del aceite es 840 kg/m3 y su viscosidad 1.6 centipoises.
ZA +Hb - HrA-B = ZB
Como ecuación final a utilizar:
HB = HrA-B + 12
HrA-B = (f( L + Le)/D)*V2/2g
V=Q/A = (0.0033 m3/s)/(0.0045 m2) = 0.73 m/s
Obtener N° de Reynolds = densidad* volumen* densidad/ viscosidad = 2.9*10^4 turbulento
f = 0.025
longitud equivalente = 106 m
HrA-B= 0.025*(300+ 106)/(0.076)*(0.73^2)/((2)*(9.8)) = 3.63 metros
Hb= 15.63 metros
potencia teorica bomba= (0.0033 m3/s)*(15.63m)*(8232N/m3)
= 425 watts = 0.425 kwatt
potencia real = pot teorica/n = 0.425 kwatt / 0.60 = 0.8 kwatt
Reflexion:
La aplicación de Bernoulli es muy útil por que nos ayuda a resolver cualquier tipo de problemas, de ella podemos obtener muchas cosas como se observo en el problema anterior que atravez de esta ecuación llegamos a obtener la potencia de una bomba.
II Parcial
Balances de materia
II Parcial
Balances de materia
Objetivos:
1) Definir un sistema y establecer fronteras del mismo
2) Explicar las diferencias entre un sistema abierto y un sistema cerrado
3) Escribir un balance general de materiales
4) Citar ejemplos donde no hay acumulación, generación, consumo o flujo de masa.
Proceso: Una serie de acciones, operaciones o tratamientos que producen un resultado.
Operaciones desde la industria química: * Operaciones con reacciones químicas
* Transporte de fluidos
* Generación y transporte de calor
* Proceso de destilación
* Adsorción de gases
* Biorreactores
Operaciones unitarias: * molienda
* sulfitacion
* clasificación
* evaporación
* cristalización
* centrifugado
Se tienen sistemas: * abiertos o continuos ( se transfiere material por la frontera del sistema).
* cerrado o por lotes ( no hay transferencia de material atravez de las fronteras)
En un sistema la acumulación será igual a:
acumulación: entra - sale + genera - consume
Estado estacionario: características del sistema no varian. Estado no estacionario: variación de las características.
Si el sistema no presenta acumulación, generación y consumo entonces el sistema se considera como:
entra = sale
Hay dos tipos de balance de materia:
1-En el que interviene reacciones químicas
son problemas que implican reacciones químicas donde se escoge un componente de cierta especie atómica o un múltiplo de este.
2-En el que no intervienen reacciones químicas
Son problemas con solución directa donde se descompone un peso o composición y que pueden resolverse por adición o sustracción.
Ejemplo:
Balance de masa
¿Cuántos kg de agua salen del espesador por cada 100 kg de lodos húmedos que ingresan?
Solución:
Base de calculo: 100 kg
entra = sale
100 kg lodo húmedo = 70 kg lodos deshidratado + ? kg agua
Despejando:
Respuesta kg agua = 30
Mezclado
Ejemplo:
En las estaciones de servicio es preciso añadir ácido sulfúrico diluido alas baterías secas a fm de activarlas. Se nos pide preparar un lote nuevo de ácido al 18.63% utilizando una disolución más débil que contiene 12.43% de H2SO4 (el resto es agua pura) y que se encuentra en un tanque. Si se agregan 200 kg de H2SO4 al 77.7% al tanque, y la disolución final tiene queser H2SO4, al 18.63%, ¿Cuántos kilogramos de ácido de batería se han preparado?
Los balances se harán en kilogramos.
Tipo de balance Acumulación en el tanque A entra Sale
Final IniciaL
H2S04 f(0.1863) - F(0.1243) = 200(0.777) - 0
H20 P(O.8137) - F(0.8757) = 200(0.223) - 0
Total P - F =200 - 0
Como las ecuaciones son lineales y sólo hay dos, podemos tomar el balance de
masa total, resolverlo para F y sustituir F en el balance de H,SO, para calcular P.
(P - 200)(0.1243) + 200(0.777) = P(0.1863)
P=2110kg ácido
Respuesta: F= 1910 kg ácido
Secado
Ejemplo:
Los peces que atrapan los pescadores se pueden convertir en harina de pescado, la cual puedeservir como alimento para animales en la produccion de carne para consumo humano o utilizarsedirectamente como alimento. El uso directo de la harina de pescado incrementa muchola eficiencia de la cadena alimenticia, pero el concentrado de proteína de pescado, principalmentepor razones estéticas, se usa principalmente como suplemento proteínico. Como tal,compite con la soya y otras proteínas de oleaginosas.
En el procesamiento del pescado, una vez que se extrae el aceite, la torta de pescado seseca en secadores de tambor rotatorio, se muele finamente y se empaca. El producto resultantecontiene 65% de proteína. En un lote dado de torta de pescado que contiene 80% de agua(el resto es torta seca), se eliminan 100 kg de agua, y se determina entonces que la torta depescado tiene 40% de agua. Calcule el peso de la torta de pescado que se introdujo originalmenteen el secador.
Base de cálculo: 100 kg de agua evaporada = W
Usaremos el balance de masa total más el de la torta seca, un componente de enlace, en
lugar del balance de agua:
0.8OA = 0.4OB + 100
porque el balance de la torta seca es un poco mas fácil de usar. El balance de agua puede servir para verificar los cálculos.
Entra Sale
Balance total: A = B +w =B + l00 > balance de masa
Balance de torta seca: 0.20 A = 0.6OB
El balance de torta seca nos da la razón entre A y B: B = 1/3A. Introducimos esta relación en
el balance total para obtener
Respuesta: A = 150 kg de torta inicial
Reflexion:
Este típo de balances implica una de las acciones muy útiles para poder apreciar las relaciones ante cambios de humedad de cualquiera de las corrientes del sistema o de las operaciones que estemos realizando por que se pueden calcular las masas de todas la corrientes de material del circuito de secado.
Cristalización
Un tanque contiene 10,000 kg de una disolución saturada de Na2CO3 a 30°C.
Queremoscristalizar de esta disolución 3000 kg de Na2CO3* 10 H,O sin agua en exceso. ¿A qué temperatura es preciso enfriar la disolución?
SOLUCIÓN
Respuesta: Se debe enfriar a 26°C
Reflexion:
Los balances de materia son muy importantes ya que son procesos que nos ayudan a contabilizar los flujos de materia en un determinado proceso industrial o las distintas operaciones que lo integran y son demasiado útiles en la industria ya que nos ayudan a medir o calcular los componentes cuando no se pueden medir sus cantidades.
III Parcial
Gases, vapores, liquidos y solidos y balances de energia
Objetivos:
Definir lo que es una propiedad, estado, equilibrio y fase.
Escribir la ley de los gases ideales y definir todas sus variables.
Calcular los valores y unidades de constantes R.
Calcular el peso especifico relativo de un gas.
Definir y usar la presion parcial el calculo de gases.
Resolver balances de materia donde intervengan gases.
Propiedad: es cualquier caracteristica medible de una sustancia por ejemplo viscosidad, densidad, temperatura presion etc.
Estados de la materia: * solido
* liquido
* gaseoso
* plasma
* condensado
Equilibrio: un estado en el que no existe tendencia alguna al cambio espontaneo.
Fase: Estado de la materia completamente homogeneo y uniforme.
Ley de los gases ideales
Cuando la distancia media entre las moléculas de una sustancia es lo bastante grande como para ignorar los efectos de las fuerzas intermoleculares y el volumen de las moléculas mismas, un gas se puede considerar como gas ideal. En términos más correctos, un gas ideal es un gas imaginario que obedece exactamente la siguiente relación:
pV= nRT
donde p = presión absoluta del gas
V = volumen total ocupado por el gas
n = número de moles del gas
R = constante de los gases ideales en las unidades apropiadas
T = temperatura absoluta del gas
Condiciones estandar de una gas dependera del sistema :
sistema T P Vespecifico
SI 273.15K 101.325Kpa 22.415 m3/kgmol
cientifico universal 0.0C 760 mmHg 22.415 L/ gmol
industrial gas natural 60 C 14.696 Psia 379.4 ft3/ lbmol
estadounidense 32 F 1 atm 359.05 ft3/ lb mol
Ejemplo:
Calcule el voumen, en metros cubicos que ocupan 40 kg de CO, en condiciones estandar.
Base de calculo: 40 kg CO2
(40 kg CO2)*((1 kmol CO2)/( 44 kg CO2))*((22.4 m3)/( 1 kg mol CO2)
Solucion: = 20.4 m3 CO2 en C.E.
Reflexion:
Este tema es muy util ya que las aplicaciones para estas leyes de los gases en la vida real se usan para predecir como se comportara un gas bajo condiciones reales a temperatura y presiones normales una aplicacion de este tema lo podemos observar en los propulsores.
Equilibrio liquido-liquido
Regla de las fases de Gibbs aplicable en sistema en equilibrio
Nos dice que F = C - P +2
F = # grados de libertad ( # propiedades independientes para las propiedades intensivas)
C = # componentes del sistema
P = # fase que pueden exixstir
Ejemplo:
Agua liquida, hielo = 1 componente, 2 fases
variables en la regla de fases: propiedades intensivas ejemplo temperatura.
propiedades extensivas ejemplo volumen
Aplicacion de la regla de las fases
Calcule el # de grados de libertad apartir de la regla de fases de Gibbs para los siguientes materiales en equilibrio.
a) benceno liquido puro
F=C-P + 2
1-1 + 2 = 2 > son las dos variables intensivas con las que se puede trabajar como ser temperatura y presion.
b) mezcla de hielo y agua
F=C-P + 2 = 1-2+2
F = 1
c) Mezcla de benceno liquido de vapor de benceno y helio gaseoso
F=C-P + 2 = 2- 2 +2
F = 2
Reflexion:
La aplicacion de la regla de grados de libertad es un tecnica que nos puede ayudar a relizar un procedimiento de una manera mas facil que culaquier otra tecnica por medio de ella solo necesitaremos distinguir las fases y componentes de un sistema, ademas nos ayuda a determinar cuantas propiedades intensivas podemos tener en un problema, que en lo personal me parecio muy sencilla de aplicar.
Densidad De Un Gas
Densidad = masa / volumen
Que puede expresarce como Kg/m3, lb/ft3, g/L
Ejemplo:
¿ Cual es la densidad del nitrogeno a 27 °C a 100kPa en unidades SI
Base de calculo: 1 m3 de nitrogeno ( 28kg/kmol) a 27° C, 100KPa
28kg/kmol*(1kmol/22.4m3)*(273K/27 + 273)*(100Kpa/101.3Kpa)
solucion = 1.12 kg/m3 a 27 °C, 100 kpa
Reflexion:
El estudio de la densidad de una gas es muy importante por que este dependera de variables como la temperatura y presiones, es por eso que se debe tener conocimiento de este tema ya que en la industria puede ser comun encontrarse con casos asi donde estaran a una determinada temperatura y presion y asi conocer en como se comportara la densidad de ese gas y si obtendremos los resultados esperados en un dicho proceso.
Balances De Energía
La energía total de un sistema corresponde a la sumatoria de tres tipos de energía:
1.- Energía Cinética: energía debida al movimiento traslacional del sistema considerado como un todo, respecto a una referencia (normalmente la superficie terrestre) ó a la rotación del sistema alrededor de un eje.
2.- Energía Potencial: energía debida a la posición del sistema en un campo potencial
(campo gravitatorio o campo electromagnético).
3.- Energía Interna: toda energía que posee un sistema que no sea cinética ni potencial, tal como la energía debida al movimiento relativo de las moléculas respecto al centro de masa del sistema o energía debida a la vibración de las moléculas o la energía producto de las interacciones electromagnéticas de las moléculas e interacciones entre los átomos y/o partículas subatómicas que constituyen las moléculas.
Calor: energía que fluye como resultado de una diferencia de temperatura entre el sistema y sus alrededores. La dirección de este flujo es siempre de la mayor temperatura a la menor temperatura. Por convención, el calor es positivo cuando la transferenciaes desde los alrededores al sistema (o sea, el sistema recibe esta energía).
Trabajo: energía que fluye como consecuencia de cualquier fuerza impulsora diferente a un gradiente de temperatura, tal como una fuerza, una diferencia de voltaje, etc. Por ejemplo, si un gas en un cilindro en su expansión mueve un pistón venciendo una fuerza que restringe el movimiento, este gas efectúa un trabajo sobre el pistón (la energía es transferida desde el sistema a los alrededores (que incluyen el pistón) como trabajo.
Definiremos el trabajo como positivo cuando es realizado por los alrededores sobre el sistema (la convención opuesta también suele emplearse; la elección es arbitraria siempre que se use de manera consistente con el resto de las definiciones: sin embargo, para evitar confusiones al leer referencias termodinámicas es fundamental asegurarse la convención adoptada)
Calculo de energía cinética y potencial
Ec = 1/2 *m * V^2
Ep = m.g.z
Ep = m.g.z
El principio que rige los balances de energía es la ley de conservación de la energía que establece que la energía no puede crearse ni destruirse (excepto en procesos nucleares). Esta ley es también llamada primer principio de la termodinámica.
Un sistema será abierto o cerrado según la masa pueda o no atravesar los límites del mismo durante el período de tiempo en que se plantea el balance de energía.
Energía inicial del sistema = Ui + Eci + EPi
Energía final del sistema = Uf + Ecf + EPf
Energía transferida = Q + W
Ejemplo de Balance De Energia
Vapor de agua ( que sirve para calentar biomasa) entra en la camara de vapor de H2O ( que esta separado de la biomasa de un reactor a 250 °C, saturado y se comdensa por completo en la camara. La velocidad de perdida de calor de la camara de agua hacia el entorno es de 1.5 KJ/S. Los reactivos se colocan ene el recipiente 20°C y al final del calentamiento el material esta a 100 °C si la carga consiste en 150 kg de material. Cp = 3.26 J / g.
¿Cuantos kg de vapor de H2O se necesitan por kg de carga?
La carga permanece por una hora.
Solucion:
Base de calculo: 1 hora
Balance de energia ΔE: Q + W - Δ((H + P + K)m )
ΔE = ΔU = Q - Δ((H)m)
ΔU = ΔH - Δ(pv)
ΔU= m*Cp*ΔT = 150 Kg*(3.26 KJ /Kg*K)*(100-20)K
ΔU = 39,120 KJ = ΔE
Q = -1.5 kJ/S*3600seg/h* 1 h = - 5400 kJ
ΔH vapor de agua = 1701 kJ/Kg ---> tabla de vapor saturado
Ya obteniendo los valores necesarios se sustituye en la siguiente ecuacion y se realiza un despeje para la masa
ΔE = Q - Δ((H)m)
39,120 KJ = - 5400 kJ -(-1701 kJ/Kg*mvapor H2O)
m= 26.17 kg/h
Pero se necesita saberlo por carga de agua
mvapor/mcarga = 26.17 kg / 150 kg
solucion = 0.17 kg vapor de H2O / kg carga
Reflexion:
Este tema es muy fundamental ya que este estudia otra de las leyes fundamentales de la Ingeniería Química como es la ley de conservación de la energía y también porque los balances de energía tienen gran importancia y muy amplia utilización en procesos industriales donde es preciso calentar, enfriar o aislar térmicamente, lo que ocurre en la mayoría de los casos. Mediante uno de estos balances podemos darnos cuenta si un proceso industrial necesita que le suministremos energia o si va a calentar desprendiendo calor, etc.
Presentacion de mural de dia de la tierra
El viernes 21 de abril se llevo a acabo la celebracion de el dia de la tierra donde diferentes carreras participaron atravez de la realizacion de murales y alfombras, nuestra clase de fisicoquimica participo con la presentacion de un mural que consistio en utilizar materiales reciclados y la expresion de como esta siendo afectado nuestro planeta entre mas pasa el tiempo que se manisfesto por medio de un reloj de arena hecho de varios materiales reciclados, donde finalmente nuestro mural fue ganador de el tercer lugar.
No hay comentarios:
Publicar un comentario